10.1 Introduction
This section is the initial deliverable of the FpML Pricing and Risk Working Group (PRWG).
Included in this section are:
- A very brief introduction to derivatives pricing and risk, and how this specification relates to those processes.
- The scope of the initial deliverable
- The requirements to address that scope
- A high-level overview of the structures in the schema used to address the requirements.
- A more detailed explanation of the usage scenarios together with examples
- A short glossary
10.2.1 Pricing
Interest rate derivatives are typically priced (a.k.a. “valued”) by forecasting the future price and price evolution of the assets that underlie the derivative, using these forecasts to estimate the future cash flows of the derivative instrument, and then discounting these cash flows to the preset.
For example, interest rate swap cash flows are typically calculated based in part on an floating interest rate index (such as US Dollar 3 month LIBOR). An interest rate swap’s value is usually estimated by forecasting the floating rate (in this example, USD-LIBOR-3M), calculating the forecast cash flows, and then discounting them to the present using a discount curve.
More complex products such as option products frequently use a similar process, but price the instrument under a variety of forecasts and estimate the value of the derivative by averaging or otherwise combining the various forecasts.
This specification describes ways to represent the data that is needed for generating these forecasts, if required for valuation reporting.
10.2.2 Valuation and Risk Reporting
A series of values (“measures”) can be computed about derivatives. The measures include:
- a variety of price-like values (e.g. Net Present Value, Clean Price, Dirty Price, Accrued Interest, Cash Payable, etc.),
- the sensitivities of some of the above values (particularly the NPV) to changes in pricing assumptions
- other risk measures, such as Potential Exposure, Value At Risk, etc.
The specification provides way to represent these measures and if desired to describe them in some detail.
The Pricing and Risk scope for FpML 4.2 Working Draft is:
Valuation and basic risk on the following products:
- Vanilla IR Swaps (single and dual currency fix/float swaps, non-CMS/CMT)
- Valuation reporting (trades only)
- Market Data (Yield Curves, FX spot rates)
- Market risk reporting (Delta Risk vs. Curve Inputs, FX exposures) for trades
- Credit Default Swaps
- Valuation reporting for trades
- Market Data (ir curves, credit spread, recovery rate, probability of default)
- Market risk reporting (risk with respect to. the above variables) for trades
- IR Caps/Floors/ EuropeanSwaptions, and corresponding risk types
- Valuation reporting for trades
- Market data (volatility surfaces)
- Market risk reporting
- Volatility/Vega Risk
- Convexity/Gamma Risk (applies to all products)
- Time Decay/Theta (applies to all products)
- Portfolio level valuation and risk
- Valuation
- Risk reporting
The Pricing and Risk Working Group has also provided some definitions that might be useful for other types of valuation and risk reporting.
10.4.1 Introduction
The aim of the FpML Pricing and Valuations Working Group (PRWG) is to define a set of extensions to the FpML schema that allow the description of:
- A request to provide valuation and risk information about a trade or group of trades, henceforth referred to as a Valuation Request.
- A report providing valuation and risk information about a trade or group trades, henceforth referred to as a Valuation Report.
10.4.2 Usage Scenarios
The intended uses of this specification include:
- Submitting valuation requests by relatively unsophisticated clients to more sophisticated providers, and returning the results.
- Submitting valuation requests from sophisticated trading users or applications to a valuation engine or system.
- Providing sensitivity results with a variety of levels of rigor and definitional detail
- Communicating market data between clients and providers for the purposes of either requesting valuations or explaining how valuation results were obtained.
These scenarios are described below in more detail in the “Use Cases and Examples” section.
10.4.3 Product Coverage
The products to be supported are those covered by the FpML 4.0 specification. However, we will in particular focus on the following product groupings:
- Vanilla IR Swaps (single and dual currency fix/float swaps, non CMS/CMT)
- Credit Default Swaps
- IR Caps/Floors and European Swaptions.
10.4.4 Valuation and Risk Measures
The specification and reporting of following valuation and risk measures are to be supported:
- Net Present Value
- Market Risk Sensitivities, including, but not limited to:
- Interest Rate Delta (Sensitivity to Curve Inputs)
- Interest Rate Delta (Sensitivity to Forward Rates)
- Interest Rate Vega
- Interest Rate Gamma
- FX Spot Sensitivity
- Credit Spread Sensitivity
- Sensitivity to Probability of Default
- Recovery Rate sensitivity
In addition, the schema should be easily extensible to allow additional valuation or risk measures to specified and reported.
10.4.5 Market and Pricing Data
The schema should allow the description of market or pricing data. Here we refer to market data as observable market rates or prices in some structured form (e.g. a yield curve of interest rates), and pricing data as market data that has been processed in some way (e.g. a term structure of discount factors).
This market and pricing data may be referred to by the Valuation Request as data to be used in calculating the requested valuation and risk measures, or can be included in the Valuation Report as data used to produce the reported valuation and risk measures.
In addition, a Valuation Request may refer to market and pricing data (as a group) by reference (e.g. an identifier denoting ‘use current market data’ or ‘use yesterday’s end-of-day market data).
10.4.6 Valuation Scenarios
The schema should allow the specification of shocks to one or more market data elements, collectively referred to as a Scenario, and the calculation and reporting of all applicable valuation and risk measures in the context of the Scenario rather than the base market data.
10.4.7 Portfolios
The schema should allow specification of a Valuation Request for a single trade or group of trades, henceforth referred to as a Portfolio. A trade may be defined ‘in place’, i.e. as a complete FpML trade representation, or by reference (e.g. a trade identifier). A portfolio may be specified in the following ways:
- A list of trades defined ‘in place’
- A list of trade references
- A portfolio reference (e.g. a portfolio identifier)
- A query or logical definition (e.g. all trades with counterparty x)
10.5.1 Overview
The Pricing and Risk schema is intended to meet the requirements described above. Because the requirements include both high-level, simplified representations as well as sophisticated, detailed definitions, the schema has been designed to allow a variety of amounts of detail to be provided. It will be up to the client and the provider to negotiate minimum requirements for data as well as well as the list of maximum supported elements.
The schema has been subdivided into several subschema files, corresponding to different topic areas, to reduce the number of definitions that a user needs to review and understand to be able to use the schema. These subschema include (where x-y is the FpML version number):
- fpml-valuation-shared-x-y.xsd – This includes base types used throughout the pricing and risk schema, such as quotations characteristics, measure types, etc.
- fpml-valuation-x-y.xsd – This includes valuation result sets and related definitions.
- fpml-reporting-x-y.xsd – This include messages used for requesting and providing valuation reporting results.
- fpml-mktenv-x-y.xsd – This include definitions of market environment data structures such as yield curves, volatility matrices, and the like. It contains the largest set of definitions, but is not necessary for simple uses of the standard.
- fpml-riskdef-x-y.xsd – This includes detailed definitions of valuation and sensitivity results. They include detailed definitions of sensitivity calculations and are intended to be used by sophisticated users.
10.5.2 Shared Types
10.5.2.1 Introduction
The Pricing and Risk shared types include ways to represent valuations about single objects, such as assets or pricing inputs. They include quotation characteristics, measure types, and base level valuation structures.
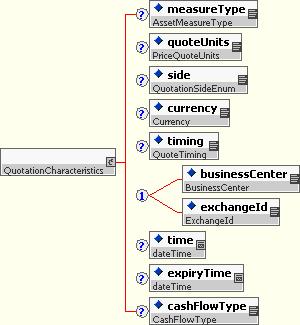
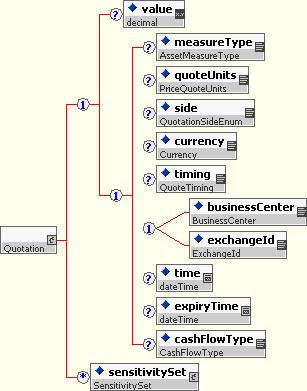
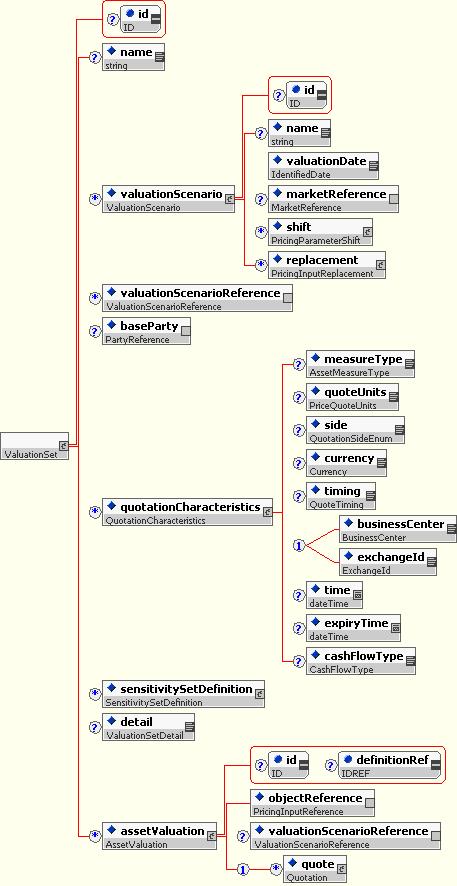
10.5.2.2 Quotation Characteristics
The QuotationCharacteristics.model model group, and the corresponding type QuotationCharacteristics, allow a variety of descriptors to be applied to any particular quotation. These descriptors include items such as:
- The measure reported (ie. The type or purpose of the quotation)
- The units of measure
- Which point of view the quotation is expressed for (buyer, seller, mid-market)
- The currency of the quotation
- Whether the quotation is for opening of business, daily high/low/mid, close of day.
- The time the quotation was recorded.
- How long the quotation remains valid
- For cash flow quotations, the type of cash flow. (This is a sub-measure; in a future draft this may be generalized further).
The Quotation Characteristics structures are used relatively consistently throughout the schema to describe values that may be reported.
10.5.2.3 Measure Types
“Measure Types” are represented by the “AssetMeasureType” type, which is an FpML scheme. A wide variety of measures have been defined (see “scheme values” for more information), but additional ones could also be defined. Current measures are divided into three broad categories:
- Valuation measures, such as NPV, cash, accrued interest.
- Sensitivity measures, such as InterestRateBucketedSensitivity
- Risk measures, such as Value at Risk.
Please see the FpML “schemes” documentation for a complete list of the measures. A number of measure types have been defined for areas beyond the current scope of this working group.
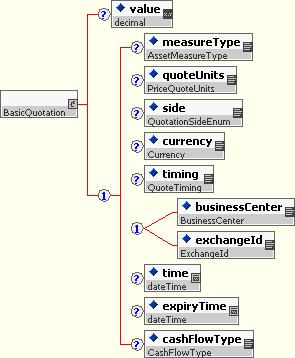
10.5.2.4 BasicQuotations
A BasicQuotation is a type that provides a value with a set of QuotationCharacteristics as defined above.
A BasicQuotation is provided for quoting simple assets where sensitivities are not required, e.g. for quotes for input instruments in curves
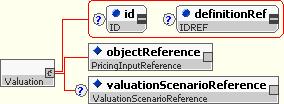
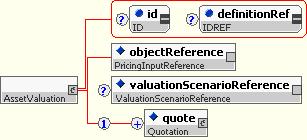
10.5.2.5 Valuation
Valuation is a type used as a base for types that represent valuations, i.e. quotations associated with objects for a particular valuation scenario.
It includes:
- An object reference, which identifies the object that is valued.
- An optional valuation scenario reference, which identifies the valuation scenario that this valuation is for.
Valuation is extended for objects such as assets and pricing structures.
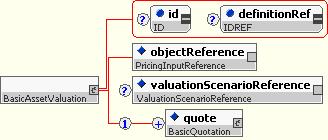
10.5.2.6 Basic Asset Valuation
A BasicAssetValuation object extends the Valuation type with a BasicQuotation. It is used for representing basic valuations of assets such as benchmarks assets used as inputs to a yield curve. It is not typically used for reporting values of derivative instruments.
10.5.3 Valuation Sets and related definitions
The following types are used to represent valuations of assets and the corresponding sensitivity valuations. These definitions are mostly contained in the fpml-pr-x-y.xsd subschema file.
10.5.3.1 Quotation
The Quotation type is similar to the BasicQuotation but also allows a collection of sensitivities to be added. This allows sensitivities to be associated directly with a specific measure, to provide a precise relationship between the sensitivities and the base value. (Note that both the base value and the sensitivities are optional, so that only one or the other could be reported.)
10.5.3.2 Asset Valuation
The AssetValuation type extends the Valuation types with a full Quotation. It allows values (and the associated sensitivities) to be represented for a single asset, such as a trade or a portfolio.
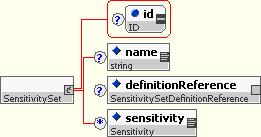
10.5.3.3 Sensitivity Set
A Sensitivity Set is collection of sensitivities, normally related somehow. It is used for containing a mini “risk report” for a single asset, e.g. bucketed interest rate delta risk for a trade or portfolio.
It can contain:
- The name of the sensitivity sets, used to describe its purpose to a human.
- A reference to the definition of the sensitivity set, used to fully explain the meaning of the sensitivities
- A collection of sensitivities.
10.5.3.4 Sensitivity
A sensitivity is a structure that contains a numerical result for the sensitivity of a valuation to a pricing input change:
It contains only a single numeric value. The associated valuation is obtained via containment (i.e. the sensitivity is directly under the same quotation structure). It has two optional attributes: A name, which is a human-readable description of the sensitivity value (e.g the “2Y” point on an interest rate delta curve), and a definitionRef, which is a reference to a Sensitivity Defintion (described in detail below). At least one of these two attributes must be filled it.
The units of the sensitivity (and other quotation characteristics) can be provided via the Sensitivity Definition or the Sensitivity Set definition. If a quotation characteristic is provided at both levels, the finer grained one (ie. that applying to the SensitivityDefinition) prevails.
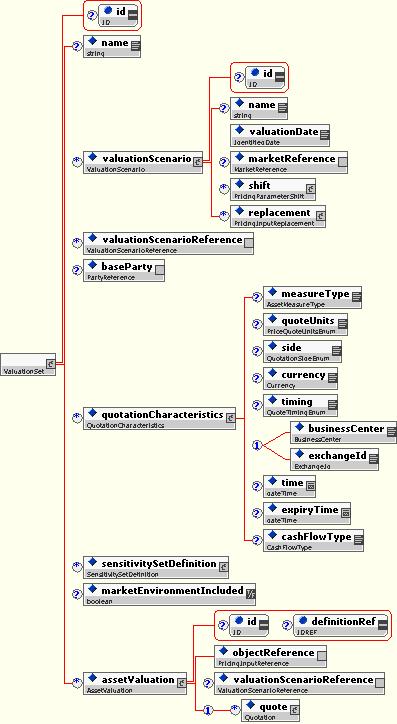
10.5.3.5 Valuation Set
The valuation set, in effect a short “risk report” or “valuation report”, is a collection of valuations, together with some identifying and descriptive information.
Contents include:
- The name of the valuation set, for human readers
- The valuation scenario that was applied (this describes items such as valuation date, the base counterparty, and the market environment).
- The base party, from which point of view the valuations are computed.
- The default quotation characteristics (used to abbreviate large valuation sets containing many similar quotations, such as NPVs).
- The definitions of any sensitivity sets, ie. definitions of the sensitivity risk reports provided.
- A flag indicating whether the market environment is or should be included.
- A collection of asset valuations, as described above.
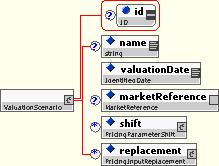
10.5.3.6 Valuation Scenario
The Valuation Scenario is a type that is used to define how the valuation was (or is to be) computed. It specifies the input assumptions for the valuations.
It includes, or can include:
- A name, for humans to understand the purpose.
- The date for which the valuation is performed.
- A reference to the market environment (see below).
- Constructs for defining how the base market environment is to be adjusted prior to valuation. (See below in risk definitions for more detail.)
10.5.4 Pricing Inputs
10.5.4.1 Overview
This section describes representations for market inputs, such as yield curves and volatility matrices. These market inputs may be shared for the purpose of requesting a valuation or of reporting how a valuation was obtained.
Market inputs are divided into two main types:
- Pricing Structures provide a name/identifier to allow the pricing input to be referenced and identified, but provide no values.
- Pricing Structure Valuations provide values (inputs and/or outputs) for a pricing structure. They are typically associated with a particular valuation scenario.
Each of these is specialized into a variety of pricing input structures, which are in turn built out of building blocks such as TermCurves (for representing term structures) and Underlying Assets with quotations.
A collection of pricing inputs is defined by a “market” or “market Environment.”
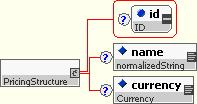
10.5.4.2 Abstract Structures
The Pricing Structure type is used as a placeholder for identifying a pricing input, such as a curve or matrix. It is extended for particular pricing structures.
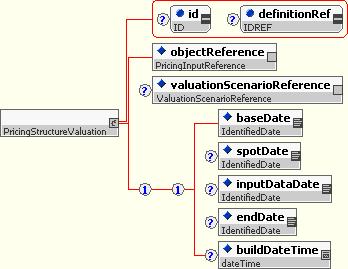
The Pricing Structure Valuation type is used to hold valuations associated with the pricing structure. It includes
- A reference to the pricing structure that is valued.
- A reference to the valuation scenario that this is for
- A variety of pieces of date information to describe the valuation.
10.5.4.3 Term Points and Curves
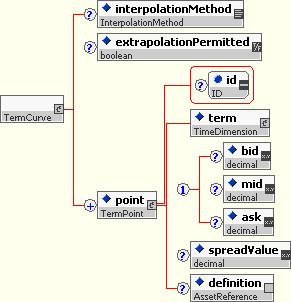
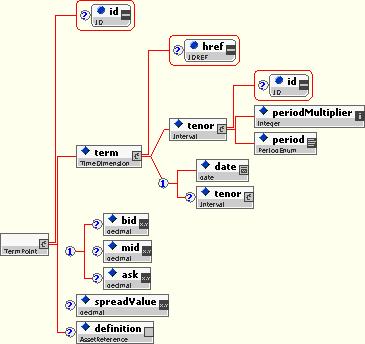
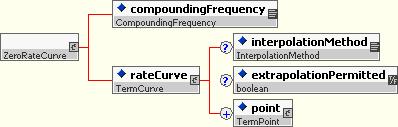
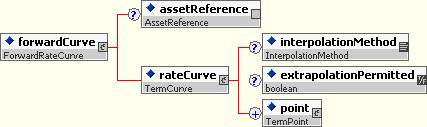
A term curve is a building block structure used to represent a set of market values over a term structure. It contains a set of Term Points, as well as some information about interpolation and extrapolation. It is used for representing term structures such as discount factor curves.
The Term Point allows bid, ask, mid, and spread values to be specified for a particular term. The Term is in turn defined as a tenor and/or a date.
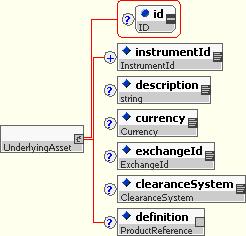
10.5.4.4 Underlying Assets
Underlying assets are used to represent simple benchmark assets, in this case for constructing market inputs such as curves. Underlying assets have a number of shared attributes:
Most of the shared elements of an underlying asset are self-explanatory. The “definition” element allows a reference to a full FpML product definition for the instrument, to allow a more complete definition to be provided.
In addition, a variety of specialized underlying assets have been produced, including, for example:
- Bonds – typically used for government bonds
- Cash – used to represent currency assets that need to be discounted
- Deposit – used to represent simple term deposits
- FxRate – used to represent FX spot rates used to build pricing inputs (like FX forward curves)
- RateIndex – used to represent interest rate indexes, such as Libor.
- SimpleFra – used to represent Floating Rate Agreement rates used to construct yield curves.
- SimpleIrSwap – used to represent benchmark Interest Rate Swaps used to construct yield curves.
These are all contained in the fpml-asset-x-y.xsd schema file.
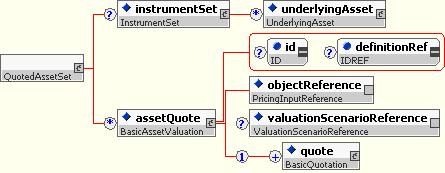
10.5.4.5 Quoted Asset Sets
The quoted asset set allows a set of underlyingAssets to be created and quotations to be provided for them:
It is used for calibrating pricing inputs, such as yield curve inputs, and for providing a set of quotes for instruments, such as FX rates, Floating Rate Index rates, etc.
10.5.4.6 Yield Curves
Yield curves are relatively complex and are divided into several types, including:
- Yield Curve – basic curve identifier
- Yield Curve Valuation – holder of valuation information about a yield curve
- Zero Curve – component of Yield Curve Valuation to hold a zero curve
- Forward Curve – component of Yield Curve Valuation to hold forward curve(s).
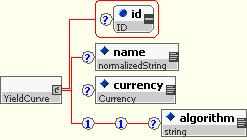
10.5.4.6.1 Yield Curve
This structure provides a high level identifier for an interest rate curve model.
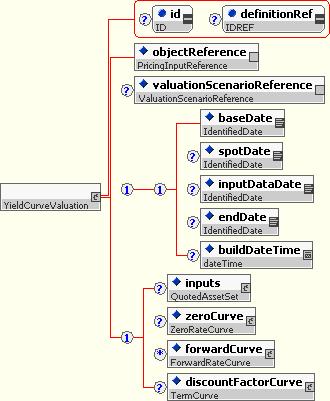
10.5.4.6.2 Yield Curve Valuation
The Yield Curve Valuation is a type of Pricing Structure Valuation that is able to hold a variety of pieces of information about an interest rate model, including:
- An optional set of input instruments used for building the yield curve
- An optional zero curve, used for representing a term structure of zero-coupon interest rates.
- An optional discount factor curve, used for representing a term structure of discount factors
- Optional forward curves, used for representing forward rate projections for specific indexes.
10.5.4.6.3 Zero Rate Curve
A zero rate curve provides a term structure of zero coupon interest rates.
10.5.4.6.4 Forward Rate Curve
A forward rate curve represents a set of forward rates for a particular floating rate index asset.
10.5.4.7 FX Forward Curves
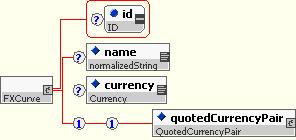
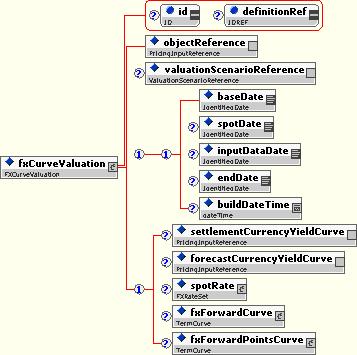
The FXCurve structure represents the abstract pricing model associated with forecasting FX rates. It extends PricingInput, adding a quoted currency pair to identify what is quoted.
The FXCurveValuation represents the valuation for forecasting FX rates. It extends PricingInputValuation.
10.5.4.8 Credit Curves
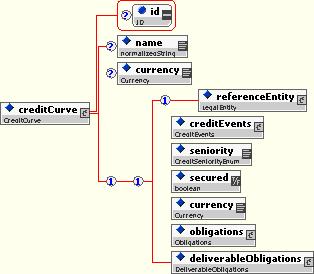
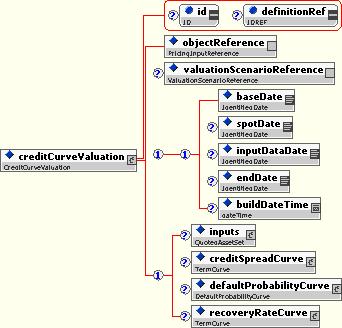
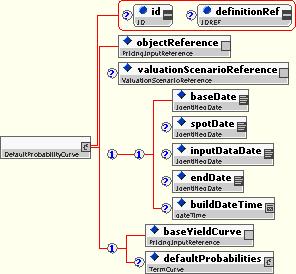
The CreditCurve structure represents the abstract pricing model associated with forecasting Credit market values (such as default probabilities). It extends PricingInput, adding several characteristics identifying the credit entity that is quoted.
The Credit Curve Valuation models the valuation of a credit curve:
The default probability curve is a special type of pricing input valuation that models the default probability of a credit entity:
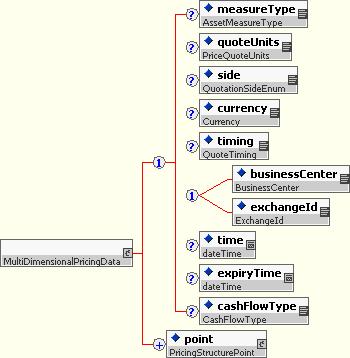
10.5.4.9 Multi-dimensional Pricing Data
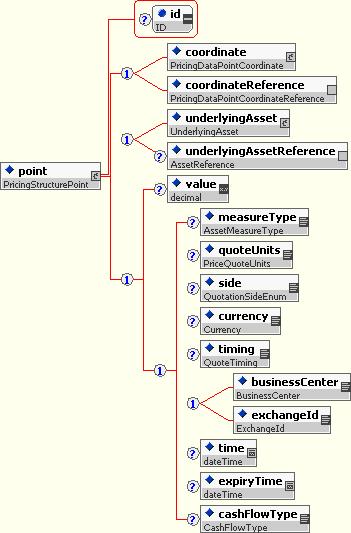
The multi-dimensional pricing data structure is used to represent complex pricing structures such as volatility matrices. It consists of a set of Pricing Structure Points.
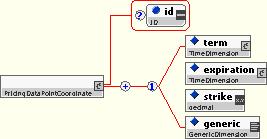
The Pricing Structure Point represents a single point of a multi-dimensional pricing structure. It provides a coordinate or coordinate reference (e.g. a combination of expiration, strike, and/or tenor), plus a value and some optional quotation characteristics.
The Pricing Data Point Coordinate allows a choice of index dimension.
10.5.4.10 Markets
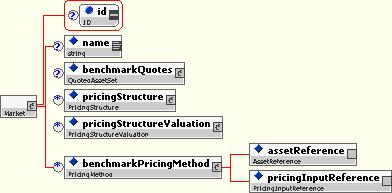
A market collects a set of the above pricing structures to provide an environment for valuing a set of assets.
It contains:
- A set of benchmark quotes for benchmark instruments, such as FX rates and IR indices.
- A set of pricing structures and their associated valuations.
- A set of benchmark pricing methods, which associate benchmark assets with corresponding pricing structures. These, for example, allow the forecast model for an interest rate index to be specified.
10.5.5 Risk Definition
10.5.5.1 Overview
The fpml-riskdef-x-y.xsd file contains definitions relating to sensitivities and valuation scenarios.
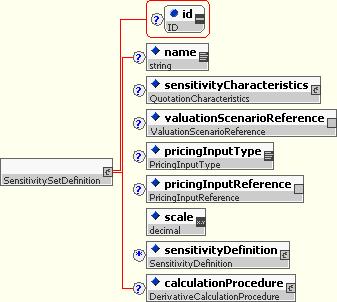
10.5.5.2 Sensitivity Set Definitions
The Sensitivity Set Definition describes a set of related sensitivities, providing a name, a set of characteristics, a reference to the valuation scenario, a reference to the pricing input (e.g. to the yield curve), and a set of definition of the individual sensitivities.
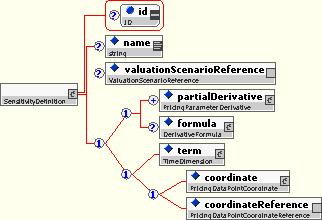
10.5.5.3 Sensitivity Definitions
The Sensitivity Definition is used to define each individual sensitivity. It can contain a name and a valuation scenario (if these are different from those of the Sensitivity Set Definition), as well as either an explicit definition of the derivatives that was computed, or a listing of the term structure point or coordinates that the sensitivity corresponds to.
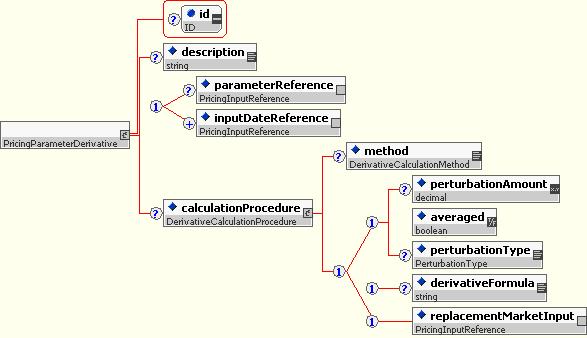
10.5.5.4 Pricing Parameter Derivative
The Pricing Parameter derivative describes a single partial derivative. It indicates the pricing parameter to which the sensitivity is computed, the units of the reported value, and how the derivative is computed (numerically or analytically).
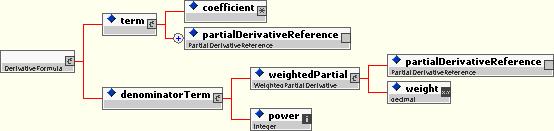
10.5.5.5 Derivative Formula
The derivative formula describes how to compute a derivative from a set of partial derivatives. It is normally only required for complex derivatives, such as Hessians, cross-gammas, etc.
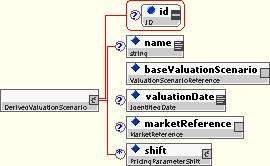
10.5.5.6 Derived Valuation Scenario
The Derived Valuation Scenario is a valuation scenario that is derived from another valuation scenario by the substitution or shift of market input data. It is used for scenario reporting, such as stress testing.
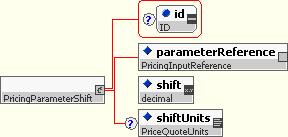
10.5.5.7 Pricing Parameter Shift
The pricing parameter shift describes how a pricing parameter can be shifted, e.g. to define a valuation scenario.
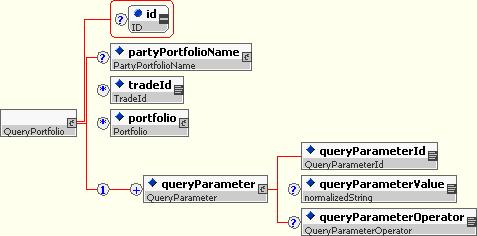
10.5.6 Query Portfolio
The QueryPortfolio type allows a portfolio to be created by grouping together trades that meet specific criteria. These criteria are defined by one or more elements of type QueryParameter. A QueryParameter contains a triplet consisting of elements of type QueryParamterId, QueryParameterValue, and QueryParameterOperator. A queryParameterId element will state a specific criteria such as product, or payment date, from a list defined by attribute queryParameterIdScheme. The queryParameterValue for that stated queryParameterId will provide a value for comparison such as swap, or 20040923, and the queryParameterOperator will define the nature of the comparison such as equals, or greater than, from a list defined by attribute queryParameterOperatorScheme.
A queryPortfolio element identified as port1 by its id attribute that is composed of swap trades with payment dates greater than 20040923 would be created using the following XML segment:
<queryPortfolio id="port1">
<queryParameter>
<queryParameterId queryParameterIdScheme="http://www.fpml.org/spec/2004/query-parameter-id-1-0">product</queryParameterId>
<queryParameterValue>swap</queryParameterValue>
<queryParameterOperator queryParameterOperatorScheme="http://www.fpml.org/spec/2004/query-parameter-operator-1-0">equals</queryParameterOperator>
</queryParameter>
<queryParameter>
<queryParameterId queryParameterIdScheme="http://www.fpml.org/spec/2004/query-parameter-id-1-0">PaymentDate</queryParameterId>
<queryParameterValue>20040923</queryParameterValue>
<queryParameterOperator queryParameterOperatorScheme="http://www.fpml.org/spec/2004/query-parameter-operator-1-0">greater than</queryParameterOperator>
</queryParameter>
</queryPortfolio>
The queryParameters within a queryPortfolio are implicitly ANDed together. Query Portfolios can also be created by defining queryPortfolio elements that are children of another queryPortfolio. In this case the child queryPortfolios are ORed together.
A queryPortfolio element identified as Port3 by its id attribute that is composed of swap, or equitySwap trades with payment dates greater than 20040923 would be created using the following XML segment:
<queryPortfolio id="port3" >
<queryPortfolio id="port1">
<queryParameter>
<queryParameterId queryParameterIdScheme="http://www.fpml.org/spec/2004/query-parameter-id-1-0">product</queryParameterId>
<queryParameterValue>swap</queryParameterValue>
<queryParameterOperator queryParameterOperatorScheme="http://www.fpml.org/spec/2004/query-parameter-operator-1-0">equals</queryParameterOperator>
</queryParameter>
<queryParameter>
<queryParameterId queryParameterIdScheme="http://www.fpml.org/spec/2004/query-parameter-id-1-0">PaymentDate</queryParameterId>
<queryParameterValue>20040923</queryParameterValue>
<queryParameterOperator queryParameterOperatorScheme="http://www.fpml.org/spec/2004/query-parameter-operator-1-0">greater than</queryParameterOperator>
</queryParameter>
</queryPortfolio>
<queryPortfolio id="port2" >
<queryParameter>
<queryParameterId queryParameterIdScheme="http://www.fpml.org/spec/2004/query-parameter-id-1-0">product</queryParameterId>
<queryParameterValue>equitySwap</queryParameterValue>
<queryParameterOperator queryParameterOperatorScheme="http://www.fpml.org/spec/2004/query-parameter-operator-1-0">equals</queryParameterOperator>
</queryParameter>
<queryParameter>
<queryParameterId queryParameterIdScheme="http://www.fpml.org/spec/2004/query-parameter-id-1-0">PaymentDate</queryParameterId>
<queryParameterValue>20040923</queryParameterValue>
<queryParameterOperator queryParameterOperatorScheme="http://www.fpml.org/spec/2004/query-parameter-operator-1-0">greater than</queryParameterOperator>
</queryParameter>
</queryPortfolio>
</queryPortfolio>
A queryPortfolio may either consist of queryParameters or other queryPortfolios, but not both.
10.5.7 Valuation Messaging
10.5.7.1 Introduction
The “fpml-reporting-x-y.xsd” subschema contains definitions relating to requesting valuations and reporting them in the form of messages.
This includes:
- TradeValuationItem
- PortfolioValuationItem
- RequestValuationReport
- ValuationReport
- PositionReport
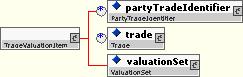
10.5.7.2 TradeValuationItem
A trade valuation item identifies a trade or trades to be valued, and contains a valuation set that describes the required valuation measures. If the trade not defined, the measures defined by the valuation set are requested for all trades in the relevant portfolio.
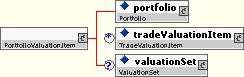
10.5.7.3 PortfolioValuationItem
A portfolio valuation item identifies portfolio to be valued, and contains a valuation set that describes the required valuation measures.
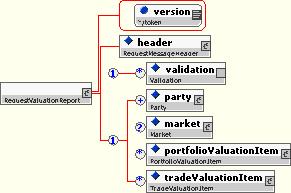
10.5.7.4 RequestValuationReport
This is a request message for requesting portfolio and/or trade valuations. It contains portfolio and/or trade valuation items that are requested.
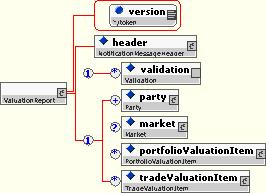
10.5.7.5 ValuationReport
This is a response message, sent in response to a “RequestValuationReport” message. It contains portfolio and/or trade valuation items and optionally market data.
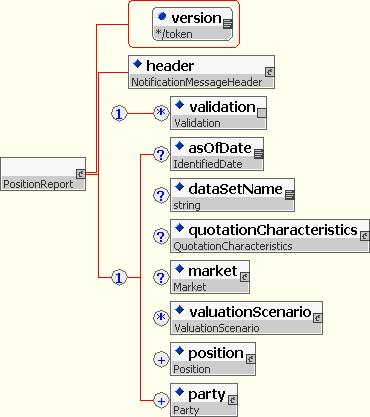
10.5.7.6 PositionReport
This is a notification message to support position reporting. It can send one or multiple positions. It implements the requirements defined by DSWG for position reports.
It contains:
- Version attribute
- Message header, giving addressing and message identification information
- An optional asOfDate, identifying the date for which the report has been prepared.
- An optional data set name, to assist subdividing a feed into multiple files.
- A set of default quotation characteristics, which can include for example the default reporting currency for NPV, the market side (mid/bid/ask), etc.
- Optional market data e.g. curves, surfaces, quotes, etc., used to generate the values in this report.
- Optional valuation scenarios used (requested/reported) in this valuation set.
- A collection of positions, including valuation information.
- The parties referenced by the trades or involved in the reporting process.
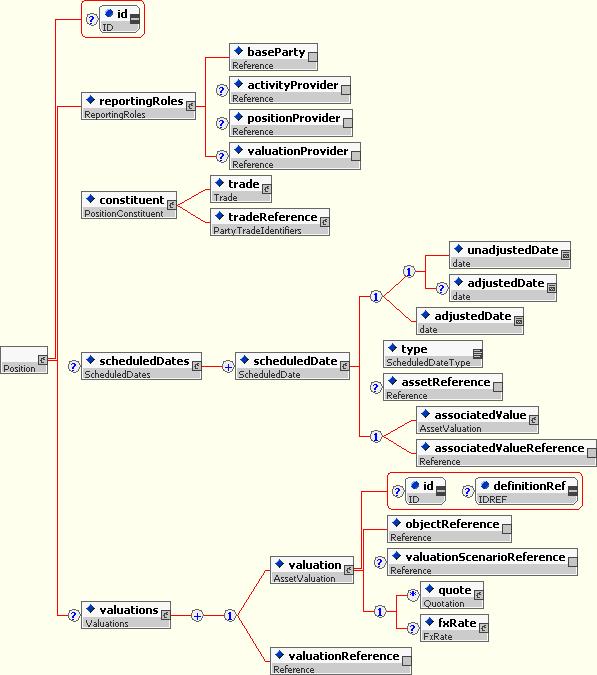
10.5.7.6.1 Position
This type is used to hold individual positions. Currently only positions based on single OTC contracts are used.
It contains:
- Information about the roles of the parties with respect to reporting the positions.
- The components that create this position, currently a trade or a reference to a trade.
- Position level scheduled dates, such as final payment dates, in a simple and flexible format.
- Valuations reported for the position, such as NPV or accrued interest. The asset/object references in the valuations should refer to the deal or components of the deal in the position, e.g. legs, streams, or underlyers.
Pricing and Risk Use Cases/Examples are available at fpml-4-2-examples.html
Many of the terms used in this document can be, and often are, interpreted in a wide fashion throughout the derivatives industry and in particular in the context of derivatives pricing and risk management systems and technology. Often, the same term may be used to convey similar but subtly different concepts in two different institutions. This section attempts to define what various common terms used within this document are meant convey.
10.7.1 Valuation
The act of calculating one or more ‘Valuation Measures’ for a trade.
10.7.2 Risk
The exposure of the value of a trade to one or more non-deterministic variables.
10.7.3 Valuation Measure
A value that can be calculated for a trade at some given point in time. Valuation Measures may be generically applicable for all trade types, for example Present Value, or may be specific to certain trade type, for example Accrued Interest or Yield. Valuation Measures may vary from one day to the next, distinguishing them from static trade information such as maturity date, counterparty etc.
10.7.4 Risk Measure
A particular type of ‘Valuation Measure’ that measures the exposure of the value of a trade to a particular variable or set of variables. Examples include Interest Rate Sensitivity, Credit Spread Sensitivity, VAR, DEAR, RAROC, Peak Credit Exposure.
10.7.5 Market Environment
A term that refers to the complete set of market data required (or available) to value a trade or portfolio. A Market Environment is made up of one more ‘Market Data’ elements.
10.7.6 Market Data
A list of related market data values that are typically grouped together for pricing purposes. Examples include an Interest Rate Yield Curve, a Credit Spread Curve, a collection of FX spot rates, a Volatility Surface, a term curve of Discount Factors or a Default Probability Curve.
10.7.7 Market Data Value
A single value associated with a particular market observable instrument or synthetically derived instrument. Examples might include the par rate for a 5 year Swap, the discount factor for a synthetic 5 year zero-coupon bond or the volatility of an At-the-Money 3-into-5 Swaption.
10.7.8 Pricing Data
Data required by a particular pricing model that is not directly associated with a market observable instrument or a synthetically derived instrument. An examples would be factor loadings for a multi-factor HJM/BGM Monte Carlo model.
10.7.9 Portfolio
An abstract definition of a group of trades.
10.7.10 Scenario
A grouping of one or more shocks to be applied to a ‘Market Environment’.
10.7.11 Sensitivity
A particular type of ‘Risk Measure’ that measures the sensitivity of the value of a trade to a change in one or more items of market data.
10.7.12 Shock
A change to be applied to a single ‘Market Data’ element within a ‘Market Environment’. The shock may affect one or more ‘Market Data Values’ within the specified ‘Market Data’ element.
10.8.1 Introduction
This section describes how to define some validation rules that cannot be enforced by the schema. It is intended as input to the Validation Working Group.
10.8.2 Reference Integrity
Intra-document references have been typed in the schema (e.g. “ValuationScenarioReference” is a reference to a ValuationScenario.) In XML schema the type of the target cannot easily be enforced; this should be enforced in the valuation rules.
10.8.3 Date uniqueness
Frequently in pricing structures (especially curves) it is not allowed to have multiple values referring to the same point. For instance, there can be only one discount factor for a single DF curve on a given date.
10.8.4 Optionality
There are many optional elements in the schema. This means that it is difficult to ensure that some kind of necessary data are present. Here are some suggested checks:
- For a given AssetValuation, a ValuationScenarioReference should be supplied either directly or in the containing ValuationSet.
- If the marketEnvironmentIncluded flag is true, a market environment should be included.
10.8.5 Names/Definitions
For sensitivities, either the name or the definitionRef attribute (or both) must be filled in. It is not easy to enforce this requirement in the schema.
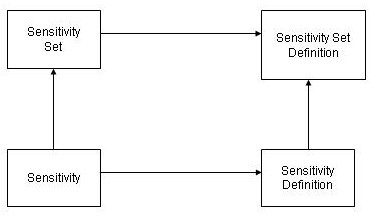
10.8.6 Consistency of definitions/references
Where there are two ways to traverse references upward through parallel structures, the resulting destination must be the same. For example, assume that a Sensitivity has a definitionRef to a SensitivityDefinition. This is contained within a SensitivitySetDefinition. If the SensitivitySet that contains the Sensitivity also has a definitionReference, it must be the same SensitivitySetDefinition as before. Following is an illustration:
Similarly, there will normally be consistency between valuation scenario references in sensitivity definitions and those in sensitivity set definitions, if they are present in both.
This section discusses issues that had particular complexity in representation, together with options for resolving these issues and a rationale for the chosen solution
10.9.1 Abstract vs. Actual Products
10.9.1.1 Issue 1: Defining an abstract product
The FpML specification deals with actual trades, that is products that have been or are in the process of being traded between two counterparties. When it comes to Valuation, there is a need for abstract deals, representing typically what the Broker market is quoting. The question is how to represent these “abstract deals”.
Options:
- Define these abstract products from scratch. This can be done in two different ways:
- a) Provide short definitions and rely on market convention. At the extreme, these could be only names, e.g. SWAPUSD-10Y. The advantage is that the task can be carried out relatively fast, counting on the fact that the number of abstract deals needed is small. The disadvantage is that relying on market conventions, can potentially lead to a disagreement between two parties.
- b) Provide a thorough definition. This would avoid ambiguity but it means the PRWG could potentially have to redo a large part of what the a FpML product group has already done.
Both of the above (a,b) cases would require that systems be enhanced to parse these new definitions.
- Reuse the FpML standard to define abstract trades. Disadvantages related to this approach include:
- a) Some elements in the FpML standard are irrelevant for abstract products (for example parties).
- b) Some elements must be “tweaked” to accommodate specificity of the abstract trades. Typically, an abstract trade is usually defined as a “sliding maturity” product (the case of futures being more ambiguous) whereas a real deal has a converging maturity. Dates accommodates the latter, tenors the former.
- c) These definitions are verbose.
- d) Some abstract deals are not defined by FpML (typically the discount factor of maturity T is a very useful concept when it comes to valuation).
- Even with the above (a,b,c,d) issues, there are noticeable advantages to this approach including :
- a) Leveraging the existing standard and reusing existing definitions, would avoid redundant work and mistakes.
- b) Enhancing systems that already process FpML to deal with abstract products is an easier task.
10.9.1.2 Issue 2: Use of tenors instead of absolute dates
The main difference of abstract deals with FpML products is that most of the times these deals are “sliding” instead of “converging”, that is their maturity is not fixed and they cannot be defined in terms of dates but in terms of “tenors”.
10.9.1.3 Issue 3: Stub definitions
In FpML, the stub is defined in terms of dates (FirstRegularPeriodStartDate...). Since in abstract deals this is not possible we must define the stubs a priori. There are implicit market conventions for these but they are rather loosely defined. A stub can be placed:
- at the beginning
- at the end
- both
The term of a stub can be:
- short, which means shorter than the regular period
- long
It is always possible to create a short stub from a long one by creating an extra-regular period. The reciprocal is true, by aggregating the short period to the next or previous regular period.
The market convention tends to refuse to have a stub that is “too” short (say 10 days).
The only reason why you would have a stub at the beginning and at the end is because the Roll Convention is not on the start or termination date.
10.9.2 Product and Trade Identification and Description
10.9.2.1 Issue 1: Trade Summaries
The example valuation and risk reports generally include some kind of trade information summary, but FpML does not currently support this type of summary.
10.9.2.2 Options:
- Create a summary view for required products.
- Include full trade details
- Reference trade via ID or xml reference.
10.9.2.3 Solution:
Reference the trade via ID or xml reference. Do not create a trade summary.
10.9.2.4 Rationale:
Trade summaries are mostly useful for humans, not computers. FpML should provide a useful, forward-looking solution, not try to mechanize the past.
10.9.2.5 Issue 2: Trade Identification
FpML allows trades to be identified by multiple external IDs (tradeIdentitifier/partyTradeIdentifier). Trades can also be identified by an internal XML document identifier (as long as the trade is in the same FpML document.).
10.9.2.6 Options:
- 1. Allow single external ID per trade
- 2. Allow multiple external IDs per trade
- 3. Use XML internal ID for each trade.
10.9.2.7 Solution:
Number 2
10.9.2.8 Rationale:
Most valuation reports will be for a large number of trades not sent in the same document, so an internal XML ID is not useful, and there is no FpML-standard document identification scheme.
10.9.3 Pricing Inputs
10.9.3.1 Issue 1: Term Representation
It will be necessary to be able to represent term structures for a variety of pricing inputs as well as for risk reports. There are a variety of ways to represent the time dimension for the term structure.
10.9.3.2 Options
- Explicit date
- Tenor (number plus period)
- Reference to another structure that contains a date.
- Number of days
- Year Fraction
10.9.3.3 Solution:
- For yield curves:
- Date is mandatory
- Tenor is optional
- Reference to another structure is optional
- Year fraction is optional
- For volatility surfaces
- Tenor is normally required.
- Date is optional.
- Reference to another structure is optional
- Year fraction is optional
- For credit spread / recovery rate curves
- Date is mandatory
- Tenor is optional
- Reference to another structure is optional
- Year fraction is optional
10.9.3.4 Rationale:
- Dates are most useful for yield curves and most explicit.
- Tenors are the market convention for credit spread curves, but use of dates as default will make the curves consistent with yield curves.
- For volatility surfaces, precise dates aren’t so important and using tenor provides better usability.
- Year fraction is a calculated value and can’t necessarily be supported by all systems.
- Number of days could be supported by using the tenor (in days).
Comment: it would be more consistent to make the same index (e.g. date) mandatory for everything. If someone wanted to roll the vol surface to another day, they could do this as long as the sender had supplied a tenor.
10.9.3.5 Issue 2: Ability to handle different dimensionality for pricing inputs
- Some pricing inputs, especially volatility representations, can vary in dimensionality. (points vs. curves vs. surfaces vs. cubes). We need to be able to accommodate this.
- There is considerable similarity across pricing inputs in the need for term structures of various dimensionality. It would be nice to reuse this.
10.9.3.6 Options:
- Separate structures for each pricing input/number of dimensions.
- Single n-dimensional structure
- Generic ability to add another term structure dimension to an existing structure.
10.9.3.7 Solution:
Generic ability to add another term structure dimension to an existing structure.
10.9.3.8 Rationale:
- Generic structure may be too abstract to handle easily.
- Separate Structures don’t provide reuse.
10.9.3.9 Issue 3: Dates used within pricing structures
For a single market input (e.g. curve), there are multiple dates that can describe the data. These include:
- Date of input points – date data was retrieved from.
- Base date – date used a base for computation. (Typical this will be the same as above, but not always.)
- Spot date – base date plus settlement lag for the currency. (“days to spot”).
- Date/time generated - the date and time the calculation was actually performed.
Which of these should be required and/or optional?
10.9.3.10 Solution:
- Base date should be required
- Input data date should be optional; normally this would not be supplied if the same as base date.
- Spot date would be optional
- Date generated would be optional.
10.9.3.11 Rationale:
- Base date is necessary for understanding the meaning of the values expressed by the curve.
- Spot date is derivable from base date.
- Input data date is normally same as base date, except in unusual cases.
- Date generated is useful for tracking and sequencing purposes, but has no other processing significance.
10.9.3.12 Issue 4: Compactness of term structure indexes
FpML architectural guidelines and standard XML modeling practice require putting business data in elements. However, for repeated numerical data like term structures, i) this produces very verbose, possibly difficult-to-read XML, and ii) the term structure indexes can be thought of as meta-data anyway, since the real data is the numerical value.
10.9.3.13 Options:
1. Indexes in elements reusing existing FpML structures, e.g.:
<dfpoint>
<date>2004-06-01</date>
<tenor>
<periodMultiplier>1</periodMultiplier>
</period>D</period>
</tenor>
<value>0.995</value>
</dfpoint>
2. Indexes in elements using more compact structures, e.g.:
<dfpoint>
<date>2004-06-01</date>
<tenor>1D</tenor>
<value>0.995</value>
</dfpoint>
3. Indexes in attributes:
<df date=”2004-06-01” tenor=”1D”>0.995</df>
10.9.3.14 Solution:
We have chosen to use the fully expanded form, but to allow referencing some of the coordinates so that the information does not have to be repeated.
10.9.3.15 Rationale:
Compromise that preserves FpML design rules but allows a more compact representation.
- solution 1: 134 characters = 3.1 x
- solution 2: 79 characters = 1.8 x
- solution 3: 43 characters = 1.0 x
10.9.3.17 Solution:
FX rates need to be treated as pricing / reporting inputs
10.9.3.18 Rationale:
FX conversion is often required in reporting values and risks.
10.9.3.19 Issue 7: Handling of credit default swap basis conventions
This applies to credit default swaps and recovery rates. Are all CDS basis conventions required for specification of credit curves?
10.9.3.20 Option 1: partial description
- Reference entity – underlying entity used to determine default condition. Should include the full name, RED identifier and/or other standard identifier. For index transactions, a unique identifier (e.g. DJ TRAC-X NA 100 Series 2)
- Debt seniority – One of the following: senior, T3 Subordinated, LT2 Subordinated, UT2 Subordinated, T1 Subordinated
- Secured – Yes / No flag if the protection is on secured debt.
- Currency – Currency of the protection payout
- Restructuring event - no restructuring, modified restructuring, modified modified restructuring, etc.
- Optional descriptor – ability to add additional terms to distinguish this set of market data
10.9.3.21 Option 2: full description:
|
Contract Term |
Description |
Options/Value |
Defaults |
|
Reference Entity |
Underlying entity used to determine default condition. Should include the full name, RED identifier and/or other standard identifier |
Text name of the underlying entity; RED identifier of the underlying entity; Other identifier of the underlying entity |
N/A |
|
Credit Event |
The material credit event. Multiple selection and at least one required. Modified Restructuring is where a Restructuring event is allowed but a Restructuring Maturity Limitation applies |
Bankruptcy; Failure To Pay; Restructuring; Modified Restructuring; Modified-Modified Restructuring; No Restructuring |
Bankruptcy; Failure To Pay; Restructuring |
|
Seniority |
The seniority of the deliverable obligation. Single selection and required. |
Senior; Sub Tier 1; Sub (Upper Tier 2); Sub (Lower Tier 2); Sub Tier 3 |
Senior |
|
Secured Flag |
Whether the deliverable obligation is secured or unsecured. Single selection and required. |
No |
|
|
Currency |
The currency of denomination of the deliverable obligation. Single selection and required. |
List of supported currencies |
USD |
|
Obligation Category |
What sort of reference payment will trigger a credit event. Single selection and required. |
Payment; Borrowed Money; Reference Obligations Only; Bond or Loan; Bond; Loan; |
Borrowed Money |
|
Deliverable Obligation Category |
What sort of obligation may be delivered in the event of the credit event. Single selection and required. |
Payment; Borrowed Money; Reference Obligations Only; Bond or Loan; Bond; Loan; |
Bond or Loan |
|
ISDA CD Definitions |
Specifies what ISDA document and supplement (if any) is applicable to this curve. Multiple selection and required. |
1999 ISDA; 1999 Successor Supplement; 1999 Convert Supplement; 1999 MR Supplement; 2003 ISDA |
1999 ISDA; 1999 Successor Supplement; 1999 Convert Supplement; 1999 MR Supplement; |
|
Deliverable Exclusions |
Security types excluded from delivery of this contract |
Exclude zero coupon; Exclude convertible; Exclude floating rate note |
None |
|
Obligation characteristics |
Types of obligations that may be considered for default determination |
Pari Passu Ranking; Not Contingent; Not Domestic Issuance; Not Domestic Currency; Not Sovereign Lender; Listed; Not Domestic Law; Specified Currency OECD; Specified Currency non-OECD |
Multiple selection |
|
Deliverable obligation characteristics |
Types of securities that can be delivered to the protection holder upon trigger of the contract |
Pari Passu Ranking; Not Contingent; Not Domestic Issuance; Not Domestic Currency; Not Sovereign Lender; Listed; Not Domestic Law; Specified Currency OECD; Specified Currency non-OECD; Accelerated or Matured; Not Bearer |
Multiple selection |
10.9.3.22 Option 3: fpml CD 4.x specification:
Refer to the existing fpml CD v4.0 specification for all references to unique terms defining CDS instruments
10.9.3.23 Solution:
Option 1: Use the partial description.
10.9.3.24 Rationale:
Simplified approach captures most relevant components for determining pricing basis. Can be expanded at a later time using the optional field (or via amendments to the specification).
10.9.4 Valuation Reporting
10.9.4.2 Options:
- Pay vs. receive?
- Cash flows on value date
- Currency translation
- Pricing currency
- Valuation date
- Underlying security or benchmark price if applicable
- Volatility and Delta if applicable
10.9.4.3 Solution:
Use Asset Measures to allow a variety of results to be returned.
10.9.4.4 Rationale:
This allows a user to extend the standard to provide more types of returned values.
10.9.4.5 Issue 2: Reporting Currency
Reporting should be in a single specified currency, with currency conversion rates and the source of those rates identified for any trades not in the reporting currency.
10.9.5 Risk Types and Measures
10.9.5.1 Issue 1: Risk types and measures
Need to specify the risk type and measure of the submitted risk figures.
Risk Types
There are a number of broad market risk types.
- Interest Rate
- Credit Spread
- FX Rate
- Equity Price
- Commodity Price
Risk Measures
For each of the broad risk types a number of risk measures are used. Risk measures are typically generated by perturbing the valuation parameters and calculating the effect on the net present value of the trades or portfolio.
- Delta, first order sensitivity to a shift in the valuation parameter
- Parallel shift (applicable to all risk types)
- 1-dimensional, bucketed risk (applicable yield curves and credit curves)
- Gamma, second order sensitivity to a shift in the valuation parameter
- Parallel shift
- 1-dimensional
- Vega
- Parallel shift
- 2 or 3 dimensional, risk against each individual entry in the volatility surface/cube
- Scenario
- A single number representing the sensitivity to a shift in the valuation parameters defined by a (separately) specified scenario
10.9.5.2 Solution
We therefore need to be label a risk figure with an entry from the following hierarchy.
- Market Risk
- Interest Rate
- Delta
- Gamma
- Vega
- Scenario
- Credit Spread
- Delta
- Gamma
- Vega
- Scenario
- FX Rate
- Delta
- Gamma
- Vega
- Scenario
- Equity Price
- Delta
- Gamma
- Vega
- Scenario
- Commodity Price
- Delta
- Gamma
- Vega
- Scenario
- Scenarios cross risk type
- Interest Rate
- Credit Risk
- Current Exposure
- Potential Exposure
For yield curves, the shifts can be performed in either
- Input Rates
- The yield curve benchmark prices
- Output rates of resulting term structure of
- The resulting term structure of implied
- Zero Rates
- Forward Rates
- Par Rates
- The resulting term structure of implied
Other valuation parameters typically do not have both input and output values.
10.9.5.3 Solution
The risk data must include a reference to the perturbed node of a valuation parameter. And the node can be an input node or an output node.
References can be either to a bucket node / matrix element or it can be reference to the full yield curve / volatility / object. In the latter case it is a parallel shift greek.
10.9.5.4 Issue2: Shift size
Shift sizes can potentially be a subject for discussion. Either we specify one standard definition or we include the shift size in the message.
10.9.5.5 Solution
In order to keep the complexity down, we define the shift sizes to be
- Delta and gamma sensitivities are based on shift size
- interest rates 1 basis point (0.01%)
- credit spreads 1 basis point (0.01%)
- Vega
- all risk types 1%
- Scenarios
- The shift size for each individual risk factor is specified in separate scenario representation which includes a large set of references to the nodes in valuation parameters and shift sizes.
10.9.5.6 Issue 3 Shift method
A number of different shift methods are used when calculating sensitivities (central differences, right hand side, scaling etc).
10.9.5.7 Solution
It is not our ambition to harmonize calculation methods but rather to reach a common understanding of the resulting numbers. We therefore leave out the applied method from the message.
10.9.5.8 Issue 4 Risk currency
The currency in which a risk figure is expressed is needed.
10.9.5.9 Solution
Typically the risk figures are expressed in the same currency as the currency of the trade. Trades involving more than one currency will have its risk expressed separately against yield curves etc for each currency. The currency element should be part of the message.